Proszę o znalezienie ewentualnego błędu, aby nie musiałem tworzyć tego silnika.
Chodźmy!
1. Jako podstawę mamy siłę odśrodkową, a także inne ciekawe zjawisko - zależność prędkości od masy.
Wyobraź sobie, że stoisz na obrotowym stojaku i obracasz się z określoną prędkością. Masz w rękach stalowe kulki i trzymasz je blisko piersi. Gdy tylko rozłożysz ręce w różnych kierunkach, zaczniesz wirować wolniej, ponieważ „masa” wzrosła, mówiąc w przenośni.
Jeśli ponownie zmniejszysz kule do skrzyni, twoja prędkość obrotu będzie taka sama.
Tak więc, niezależnie od tego, jak rzucasz piłkami i jak szybko się obracasz, energia kinetyczna nie zmienia się.
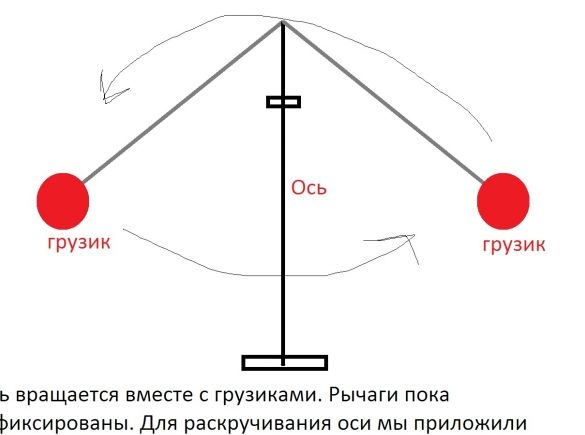
2. Teraz wyobraź sobie pionową oś, na której dwie dźwignie tej samej długości są ustawione pod kątem. Dźwignie są obniżane pod pewnym kątem, a ciężarki są instalowane na ich końcach. Po odkręceniu tego projektu dźwignie wzrosną do poziomu ich punktów mocowania z powodu siły odśrodkowej.
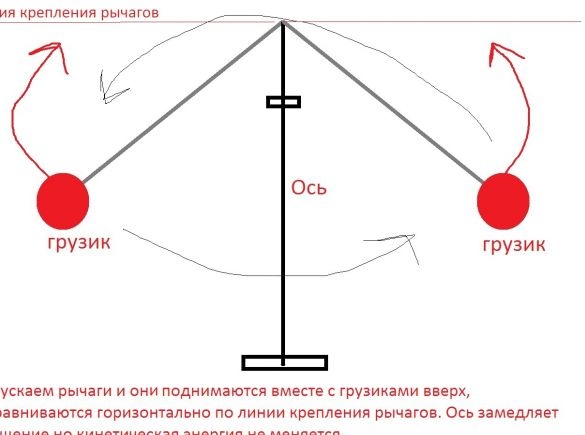
I wtedy zaczyna się zabawa. Czy energia kinetyczna całego ciała zmieni się, jeśli dźwignie z ciężarkami same się podniosą? Nie sądzę
W tym względzie mamy dziurę w prawie zachowania energii, a mianowicie energia jest pobierana znikąd. Obracamy oś za pomocą dźwigni do określonej prędkości i zużywamy pewną ilość energii kinetycznej, na przykład E1. Następnie wyłączamy blokady dźwigni, są one wyrównane wzdłuż linii mocowania, a konstrukcja zwalnia, ale energia kinetyczna się nie zmienia, możemy ją usunąć w tym samym ekwiwalencie, nazwijmy tę energię E2.
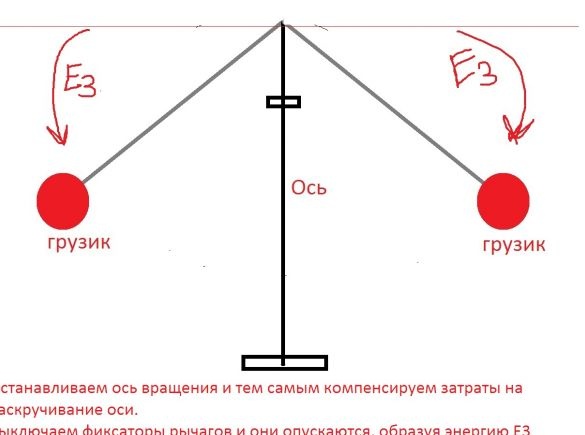
W rezultacie E1 = E2, to znaczy zainwestowana energia i strzał są takie same (nie licząc siły tarcia i innych bzdur). Otrzymujemy również darmową energię, w postaci podniesionych obciążników, zwolnij zaciski obciążników, obniżą się i powstanie energia E3, która przekracza sprawność o 100%.
Gdzie się mylę?